Connaître la performance de ses investissements reste une étape cruciale lorsqu’il est question d’investir en bourse. La calculer permet en effet de mieux cerner la qualité de son portefeuille, de définir si nos décisions d’investissements étaient pertinentes ou, au contraire, si un rééquilibrage de portefeuille est nécessaire. Voire remettre en question notre façon d’investir ? Voici 12 mesures qui vous permettront d’y répondre.
Avant de continuer …
Abonnez-vous à notre actualité et restez à jour dès qu’un nouvel article est publié !

Table des matières
Connaître ses performances boursières pour mieux investir
Pour l’investisseur, choisir dans quoi investir ne constitue qu’une partie du travail à fournir dans cette aventure qu’est l’investissement. En effet, au fil du temps, l’investisseur devra également veiller à la performance de ces investissements, pour évaluer comment ils fonctionnent ensemble au sein du portefeuille. L’objectif de ce coup de projecteur sur vos investissements est de vous aider à progresser vers vos objectifs financiers. Plus qu’un plaisir ou une passion, investir en bourse recèle bien souvent un objectif concret, qu’il s’agisse de préparer la retraite, l’avenir de ses enfants ou protéger son pouvoir d’achat.
De manière générale, un portefeuille est dit performant lorsque sa valeur augmente régulièrement au cours du temps, même si un ou plusieurs de ses actifs perdent de la valeur. C’est le principe même de la diversification : construire un portefeuille résilient … et performant.
Portefeuille performant ←→ Génère du rendement ←→ Valeur actuelle > Valeur initialement investie
Ainsi, si vos investissements ne montrent aucun gain ou que la valeur générale de votre portefeuille diminue, il sera bon de chercher à comprendre pourquoi et prendre les mesures qui s’imposent. L’avantage de cette remise en question, via l’étude de performance, sera de maintenir un portefeuille optimal dans la durée, tout en libérant du cash pour effectuer de nouveaux achats.

Pour évaluer la performance de vos investissements, vous devrez envisager plusieurs façons différentes de mesurer la performance. Les mesures que vous choisirez dépendront des informations que vous recherchez et des types d’investissements que vous possédez. La performance d’une action ne se mesure pas de la même façon que dans le cas d’une obligation.
12 indicateurs de performances pour votre portefeuille boursier
Ci-dessous, nous vous présentons 12 mesures qui nous paraissent importantes dans le cadre d’une étude de performance globale d’un portefeuille boursier. Cette liste n’a pas la prétention d’être exhaustive, mais devrait vous offrir une vue suffisamment large et globale pour constituer une bonne base de travail.
Rendement de l'actif
Étudier le rendement d’un actif revient à basculer l’évolution du prix en pourcentage. L’intérêt derrière cette transformation mathématique est double :
- C’est une valeur sans échelle, ce qui fait qu’il devient possible de comparer des investissements dont les grandeurs de prix diffèrent beaucoup (par exemple, quelques € versus plusieurs centaines d’€).
- Les séries de rendement sont plus faciles à gérer que les séries de prix, car les premières ont des propriétés statistiques plus intéressantes.
Le rendement d’un actif sur une unité de temps se calcule :

Où T est la valeur de prix à la période actuelle et T-1 la valeur de prix à la période précédente. Par exemple, s’il s’agit du rendement d’actif journalier, T correspondra au prix du jour et T-1 au prix d’hier.
Prenons un exemple avec 4 valeurs bien différentes :
- Berkshire Hathaway share A
- The Walt Disney Company
- Thales
- McPhy Energy
Volatilité de l'actif
Une fois que nous avons calculé le rendement d’un actif, il est alors question de définir sa volatilité. La volatilité d’un actif indique son degré de risque. Les actifs hautement volatils (comme les actions ou les cryptomonnaies) sont généralement plus risqués que les actifs plus stables (comme les obligations ou l’or).
Pour définir la volatilité, nous allons calculer l’écart-type, qui représente la dispersion des valeurs de prix autour d’une moyenne historique.
Le calcul se déroule comme tel :
- Calculer la moyenne arithmétique X̄ : en additionnant toutes les valeurs et en divisant cette somme par le nombre de valeurs.
- Calculer la variance σ² :
- En faisant la différence entre chaque valeur individuelle Xi et la moyenne X̄ précédemment calculée.
- En mettant chaque différence au carré
- En additionnant toutes ces différences mises au carré
- En divisant cette somme par le nombre de valeurs (n)
- Calculer l’écart-type σ : en mettant la variance σ² sous racine carrée.

En statistiques, plus l’écart-type est élevé autour de notre estimation de quelque chose, moins nous sommes certains de la vraie valeur de cette chose. En résumé, un écart-type important équivaut à une grande incertitude. Ce faisant, plus l’écart-type d’un actif est élevé, plus la probabilité que son rendement se retrouve au-dessus ou en dessous de zéro est élevée. Un actif dont l’écart-type est bas sera un actif dont la probabilité de rendement sera faible, proche de 0 %, mais de manière certaine.
Rendement d'actif moyen attendu
Le rendement d’actif calculé plus haut constitue une grille de valeurs de rendement en fonction du temps. Il est cependant également possible de moyenner cette grille pour en tirer une valeur moyenne, le rendement moyen attendu.

Cette valeur moyenne a un intérêt prédictif en ce sens qu’elle permet, sur la base de l’historique des rendements individuels, d’estimer un rendement futur (bien que les performances passées ne préjugent pas des performances futures).
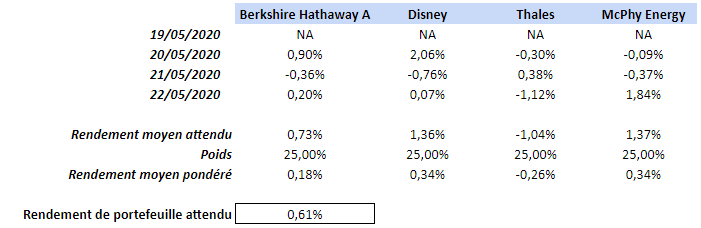
Reprenons la liste d’exemples précédente :

Rendement d'actif moyen pondéré
Il existe cependant mieux que le rendement moyen attendu. En effet, dans ce dernier chaque valeur est utilisée de la même façon que les autres valeurs. Nous parlons de valeurs équipondérées ; chaque valeur a le même poids, la même importance dans le calcul.
Il est cependant plus pertinent de donner un plus grand poids aux valeurs récentes. Par exemple, les rendements des 5 derniers jours sont probablement plus importants dans notre calcul que des rendements datant de l’an dernier (effet momentum). Par conséquent, nous devons calculer les rendements moyens pondérés.
Cette méthodologie se base sur la moyenne mobile à pondération (WMA) avec un facteur de décroissance qui diminue au fur et à mesure que la valeur devient de plus en plus vieille. Les rendements les plus récents ont donc un poids plus élevé dans le calcul de rendement moyen pondéré.

C’est cette même méthodologie qui est à l’origine des moyennes mobiles exponentielles en analyse technique (avec un facteur de décroissance qui diminue de façon exponentielle dans le temps).
Rendement de portefeuille attendu
Focaliser son attention sur les rendements individuels, c’est bien. Mais mieux cerner le rendement général du portefeuille, c’est mieux ! Dès lors, évaluons le rendement attendu du portefeuille, au sein duquel chaque actif se voit attribuer une pondération.
À partir des rendements d’actifs moyens attendus, nous pouvons désormais calculer le rendement attendu du portefeuille, via une moyenne pondérée :
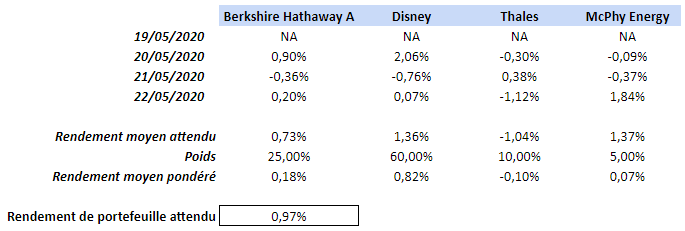
Reprenons l’exemple précédent. Imaginons un portefeuille composé des 4 valeurs utilisées dans cet article (Berkshire Hathaway share A, The Walt Disney Company, Thales & McPhy Energy). Notre portefeuille est équipondéré : chaque valeur s’est vu allouer 25 % de notre allocation totale.
Dans l’exemple, nous avons donc alloué une proportion égale à chaque action. Par conséquent, le rendement attendu du portefeuille va être calculé en calculant le produit du rendement attendu de chaque actif et du poids de l’actif :
De là, une porte s’ouvre pour optimiser votre portefeuille. En effet, en changeant uniquement la pondération des différents actifs (et en quittant l’état équipondéré), il est possible d’optimiser la composition pour maximiser ce rendement de portefeuille attendu. Par exemple :
Volatilité du portefeuille
De la même façon que la volatilité a été calculée plus haut sur les actifs, nous pouvons également calculer celle du portefeuille global. La volatilité du portefeuille est calculée en calculant l’écart-type des rendements de chaque action ainsi que la covariance entre chaque paire d’actions.
Mathématiquement, les choses se corsent. Si vous n’aimez pas les mathématiques, préparez une aspirine ! Nous avons donc :
Ce qui pourra vous sembler être du charabia revient à dire, en français, que la volatilité du portefeuille σ (son écart-type) correspond à la racine carrée de la variance σ². Cette dernière est calculée en additionnant les produits des pondérations au carré (ωi²) et des écarts-types au carré (σi²) de chaque valeur, et en ajoutant les covariances de chaque paire d’actifs (ρij).
Au plus le nombre de paires de valeurs est élevé, au plus le calcul est complexe. Par simplicité, nous limiterons l’exemple à deux valeurs ; en pratique, ce genre de calcul sur un portefeuille complet nécessitera l’emploi de logiciels ou de scripts spécialisés (notamment pour calculer la corrélation).
Partons donc d’un portefeuille composé de deux actions. L’action A vaut 10 000 € et a un écart-type de 20 %. L’action B vaut 100 000 € et a un écart-type de 10 %. La corrélation entre les deux actions a été calculée à 0,50. Compte tenu de cela, le portefeuille est équipondéré, le poids de l’action A est de 50% et pareillement pour l’action B. En introduisant ces informations dans la formule, la variance du portefeuille σ² est calculée comme suit :
Cette valeur est une mesure du risque global du portefeuille et fait partie des grands outils de la théorie moderne du portefeuille développée par H. Markowitz dans les années 1950. Il y est notamment dit que l’écart-type (et donc la volatilité) du portefeuille peut être réduit en choisissant des classes d’actifs avec une corrélation faible ou négative. D’où l’intérêt de diversifier votre portefeuille !
Nous vous proposons notre calculateur maison utilisant Google Sheets et pouvant être téléchargé gratuitement, sans risques (Fichier > Télécharger). Par sécurité, il n’est pas permis de le modifier en ligne. Il vous permet de calculer la volatilité d’un portefeuille composé de maximum 4 actifs.
Taux de rentabilité interne (TRI)
Ce taux prend en compte toutes les entrées et sorties de trésorerie au sein de votre portefeuille, en plus de ses valeurs initiales et finales. Lorsqu’il est calculé, le TRI représente le taux qui rend nulle la valeur actuelle nette (VAN) de votre portefeuille. Il vous permet donc de mesurer la véritable rentabilité de votre portefeuille.

Où Ct est le flux net de trésorerie pour la période t, C0 la valeur initiale du portefeuille et T la période totale de calcul.
Le but du jeu étant alors de résoudre l’équation pour trouver la valeur de TRI.
En pratique, le TRI se calcule assez facilement via Excel (ou équivalent) de cette façon :
- Tout d’abord, indiquez la valeur initiale de votre portefeuille comme étant négative. Notez également la date de début de calcul.
- Renseignez chaque nouveau flux de trésorerie comme une entrée (négativement) ou une sortie (positivement). Ne vous trompez pas, c’est contre-intuitif, mais c’est ainsi. Ici aussi, notez les dates.
- Faites le bilan des flux de trésorerie de votre portefeuille, en reportant positivement la valeur finale de votre portefeuille (ainsi que la date de fin de calcul).
- Calculez la valeur du taux d’actualisation via la formule TRI.PAIEMENTS sur Excel (XIRR si vous utilisez Excel en anglais), XIRR sur Google Sheets ou encore TRI.PAIEMENTS sur Open Office Calc.

Ci-contre à droite, vous pouvez voir un exemple de calcul de TRI sur Excel, via une approche d’investissement périodique. Nous commencions 2019 avec 10 000 € et nous avions ajouté chaque mois 500 €. Un besoin de liquidité en juin 2019 a induit le retrait de 1500 €. En fin d’année, le portefeuille avait atteint une valeur de 18 500 €. Le TRI s’élevait donc, pour 2019, à 33 %. Il est ensuite possible de réaliser cet exercice sur plusieurs années, voire entre années, pour établir un TRI de longue durée. Il est également possible de comparer différents portefeuilles/allocations pour déterminer laquelle vous procure le meilleur taux de rendement pondéré.
Taux de rentabilité pondéré dans le temps (TRPT)
Cette variante du TRI mesure le taux de croissance composé d’un portefeuille en éliminant les effets de distorsion sur les taux de croissance. Ces distorsions sont créées par les entrées et les sorties d’argent (les flux dont nous parlions plus haut pour le TRI). C’est le gros avantage du TRPT : il ne tient compte que de la variation de la valeur du portefeuille au cours d’une période donnée. Les dates des flux entrants/sortants déterminent le début et la fin de cette période, et les flux n’ont donc plus d’influence sur le rendement.
Cependant, ce TRPT n’est pas adapté pour l’investisseur particulier. Il a plutôt vocation à être utilisé par les gestionnaires de fonds qui ne maîtrisent pas les entrées/sortie de fonds ni le moment où les achats se font. La composante de temps a donc toute son importance pour eux. Pour creuser sur le sujet du TRPT, nous vous redirigeons vers cet article de la Royal Bank of Canada.
Ratio d'information
Nous avons déjà parlé de ce ratio lorsque nous vous présentons des ETF ou des stratégies passives d’investissement. Il est également utile lorsqu’il s’agit de benchmarker un portefeuille par rapport à des indices boursiers.

Le ratio d’information est égal à la différence entre le rendement moyen du portefeuille et celui d’une référence, divisée par l’erreur de suivi (qui équivaut à la différence de volatilité entre le portefeuille et la référence). Rendement & volatilité étant calculés comme expliqué plus haut.
Il aide à comprendre le niveau de risque pris pour atteindre le rendement excédentaire par rapport à une référence (ici, un indice boursier). Si le ratio d’information est positif, c’est que votre portefeuille a réussi à surperformer l’indice de référence que vous aurez choisi, compte tenu du risque relatif vis-à-vis de cet indice.
Notez que ce ratio peut également se calculer pour un actif seul.
Ratio de Sharpe
Autre ratio dont nous parlons fréquemment sur Investiforum, le ratio de Sharpe permet de comprendre le rendement d’un investissement par rapport à son risque propre.

Le ratio de Sharpe se calcule en prenant le rendement moyen réalisé par le portefeuille (Rp) duquel est soustrait le rendement d’un actif sans risque (Rf, le rendement des obligations d’état AAA par exemple). Le tout, divisé par la volatilité du portefeuille (σp).
Un ratio de Sharpe élevé sera une bonne mesure de la qualité de votre portefeuille puisqu’il permettra de savoir s’il vous permet d’obtenir un rendement supérieur aux obligations d’états, mais avec davantage de risque.
Ainsi, un ratio supérieur à 1 voudra dire que votre prise de risque est largement récompensée par un excès de rendement. Entre 0 et 1, l’excès de rendement sera balancé/annulé par une prise de risque importante, ce qui n’est pas idéal. S’il est négatif, cela signifiera que votre portefeuille est moins rentable qu’un actif sans risque (pour une prise de risque, elle, plus élevée). En conclusion, plus le ratio sera élevé, plus le portefeuille sera performant.
Ici aussi, notez que ce ratio peut être calculé pour un portefeuille comme pour un actif seul.
Ratio de Treynor
Moins connu, le ratio de Treynor permet d’embrasser la diversité du risque d’un portefeuille composé d’actifs variés. Il ressemble au ratio de Sharpe, mais le risque n’y est plus exprimé au travers de la volatilité. Cette dernière est remplacée par le bêta du portefeuille, qui mesure la tendance du rendement d’un portefeuille à changer en réponse aux changements de rendement pour l’ensemble du marché. On parle de risque systématique.

Le ratio de Treynor se calcule en prenant le rendement moyen réalisé par le portefeuille (Rp) duquel est soustrait le rendement d’un actif sans risque (Rf). Le tout, divisé par le bêta du portefeuille (βp).
Son interprétation est la même que pour le ratio de Sharpe : plus ce ratio de Treynor sera élevé, plus votre portefeuille présentera une rentabilité intéressante par rapport au risque couru par le marché dans son ensemble.
Ici aussi, notez que ce ratio peut être théoriquement calculé pour un portefeuille comme pour un actif seul. En pratique, il n’a de sens que pour un portefeuille.
Alpha de Jensen
À l’instar des ratios de Sharpe ou de Treynor, l’alpha de Jensen (souvent raccourci à alpha) calcule la différence entre le rendement réel du portefeuille et celui du marché. Si votre portefeuille surperforme le marché en même temps que le risque, nous pourrons dire qu’il génère de l’alpha.
Dans le contexte du modèle d’évaluation des actifs financiers (MEDAF), l’alpha se calcule comme suit :

En utilisant le rendement moyen réalisé par le portefeuille (Rp), le rendement d’un actif sans risque (Rf), le bêta du portefeuille (βp) et le rendement moyen réalisé par le marché (Rm).
L’interprétation de l’alpha de Jensen ressemble à celle des ratios de Sharpe et de Treynor : si l’alpha est positif, le portefeuille surperforme son marché de référence ; s’il est négatif, le portefeuille est moins performant au regard du MEDAF.
Conclusion
Mesurer la performance d’un portefeuille peut donc se faire de multiples façons. Il existe en effet tout un tas d’indicateurs et de formules pouvant apporter telle ou telle information sur le rendement, la volatilité, la surperformance, etc. Ces 12 indicateurs, non exhaustifs, devraient vous permettre de brosser un beau portrait de départ de votre portefeuille. N’hésitez pas, par la suite, à creuser le sujet pour trouver des indicateurs supplémentaires (tel que le ratio de Sortino).
Nous reviendrons ultérieurement sur certains indicateurs et nous vous présenterons des outils (notamment développés pour Investiforum) permettant de calculer, en pratique, cette performance.
Articles similaires:
- L’analyse CAN SLIM : trouver des actions à haut potentiel de gains
- Risque de récession en 2022 : actions, secteurs & stratégies à privilégier pour la fin de cycle
- Être payé pour apprendre à investir 30 minutes par jour ? C’est possible !
- Débutant en bourse ? Voici 30 statistiques clés pour bien analyser une action





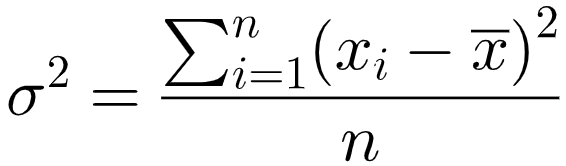
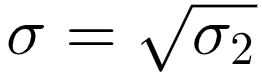


je regardais le TRI et le TRPT aujourd’hui et je me demandais lequel prendre pour quel type d’invest. Au final, je pense que pour des invests types crowdfunding/lending, le TRPT semble le + adapté comme on ne fait pas de timing avec ce type d’invest. En bourse où l’on va faire du timing, le TRI semble le + adapté, mais pour de l’investissement type DCA, peut être plutôt du TRPT par contre. Qu’est ce que tu en penses? Pas simple de savoir quel est le métrique le + adapté pour quel type d’invest.
Hello Tiri 🙂
Merci pour ton commentaire. C’est une bonne question qui m’a bien occupé aussi 😀
Le TRI prend en compte le moment et le montant des flux de trésorerie entrants et sortants. Donc pour des investissements qui impliquent des flux de trésorerie irréguliers, c’est adapté, car il permet de comparer des investissements ayant des montants et des timings différents.
Le TRPT, quant à lui, ne prend pas en compte le moment spécifique des flux de trésorerie, mais plutôt le temps écoulé entre les flux de trésorerie entrants et sortants. Le TRPT est souvent utilisé pour évaluer des investissements boursiers, où les flux de trésorerie peuvent être réguliers mais pas nécessairement constants.
En général, le TRI est plus adapté pour évaluer des projets d’investissement à long terme qui ont des flux de trésorerie irréguliers, tandis que le TRPT est plus adapté pour évaluer des portefeuilles de titres ou des fonds communs de placement où les flux de trésorerie peuvent être réguliers. Si tu investis dans des projets de crowdfunding avec des flux de trésorerie irréguliers, le TRI peut être plus adapté. Si tu investis dans des actions boursières avec des flux de trésorerie plus réguliers, le TRPT peut être plus adapté.
Je ne sais plus pour quoi j’étais parti sur le TRI plus spécifiquement pour mon suivi général d’investissements. En pratique, je track les deux, mais je reporte le TRI dans mes suivis !
J’espère t’avoir éclairé 🙂
Oui tes definitions correspondent à ce que j’ai pû lire. Le truc, c’est que J’avais crû comprendre que le TRI, oui on prend les flux de trésorie en effet, mais que c’était justement aussi ça que l’on voulait évaluer: Est ce que mon timing d’entrée/sortie est bon ou pas. Mais en fait c’est dans le sens où on pondère la performance avec la taille du capital. Cette page est bien faite je trouve: https://www.tfoco.com/en/insights/articles/internal-rate-versus-time-weighted-rate-of-return
Compliqué cette affaire 😀 . je crois que je me suis trop pris la tête avec cette histoire ahah. Merci en tout cas 🙂 .
Merci pour le lien, j’y jetterai un œil 🙂
Sympa en effet ! Je vais y réfléchir, ça sera surement changé pour la prochaine revue de portefeuille 🙂
Merci 😀